Zero ou Raiz da Função Polinomial do 1° Grau
Dada uma função afim definida por 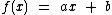 , com
, com 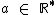 e
e 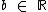 , temos que o zero ou raiz desta função é o valor de x que a anula, isto é, é o valor de x para o qual f(x) = 0, ou em outras palavras, o valor de x que torna y = 0;
, temos que o zero ou raiz desta função é o valor de x que a anula, isto é, é o valor de x para o qual f(x) = 0, ou em outras palavras, o valor de x que torna y = 0;
Vamos analisar o gráfico da função 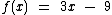 que temos abaixo
que temos abaixo
Podemos notar que no ponto (3, 0), pertencente ao gráfico da função, temos o valor de x, que neste caso é 3, anulando a função, ou seja, cuja ordenada (y) é igual azero. Então x = 3 é a raiz da função.
Toda função 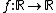 na forma
na forma 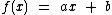 possui uma única raiz
possui uma única raiz
Determinando a Raiz de uma Função Polinomial do 1° Grau
Vamos determinar algebricamente a raiz da função 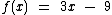 que vimos acima.
que vimos acima.
Para que um valor x seja raiz da função, é preciso que tenhamos f(x) = 0.
Vamos realizar tal substituição na lei de formação da função:
Note que obtivemos uma equação do primeiro grau, portanto para determinarmos o valor de x basta que a solucionemos:
Como já era de se esperar, para y = 0 temos que x = 3, o que nos leva ao ponto (3, 0), pertencente ao gráfico da função, como vimos destacado no gráfico anterior.
Resumindo, para determinarmos a raiz de uma função afim basta substituirmos o f(x) ou y da regra de associação da função, por 0 e solucionarmos a equação do primeiro grau encontrada, obtendo assim a raiz da função.
Função Crescente e Decrescente
Como o gráfico de uma função afim é uma reta, ela é crescente ou decrescente para qualquer elemento do seu domínio, mas como isto não acontece para todas as funções, o conceito de função crescente e de função decrescente é aplicado a intervalos do domínio da função.
Função Crescente
Uma função é crescente em um dado intervalo [x1, x2] do seu domínio quando tivermos a seguinte implicação
Ou:
Podemos ver no gráfico abaixo que quando aumentamos o valor de x, o valor de f(x), isto é, o valor de y também aumenta.
Função Decrescente
Uma função é decrescente em um dado intervalo [x1, x2] do seu domínio quando tivermos a implicação a seguir:
Referência: http://www.matematicadidatica.com.br/FuncaoAfimVariacaoSinal.aspx

Referência: http://www.matematicadidatica.com.br/FuncaoAfimVariacaoSinal.aspx


Nenhum comentário:
Postar um comentário